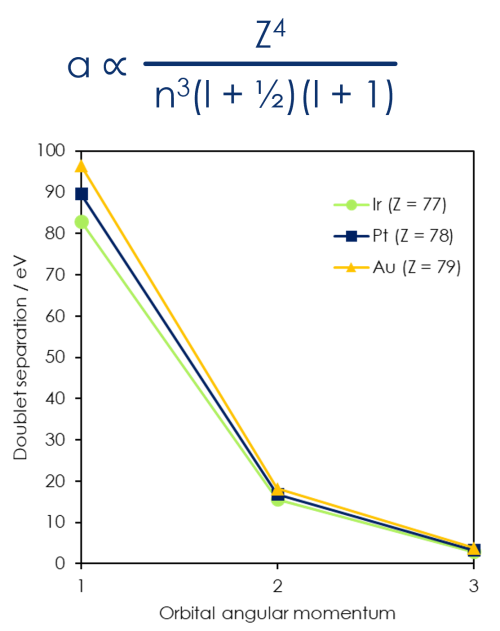XPS for Beginners
- XPS Course Fundamentals
- Data Analysis
- Applications of XPS
- Related Techniques
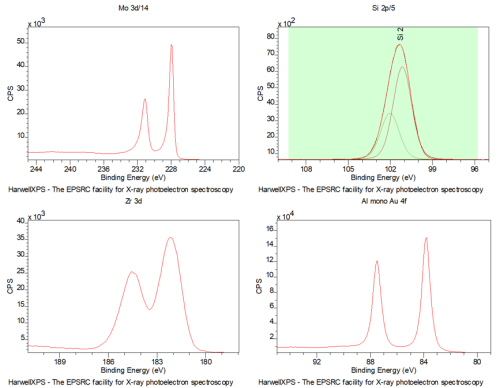
Doublets are commonly observed in XPS analysis
In fact only S-orbitals produce single peaks!
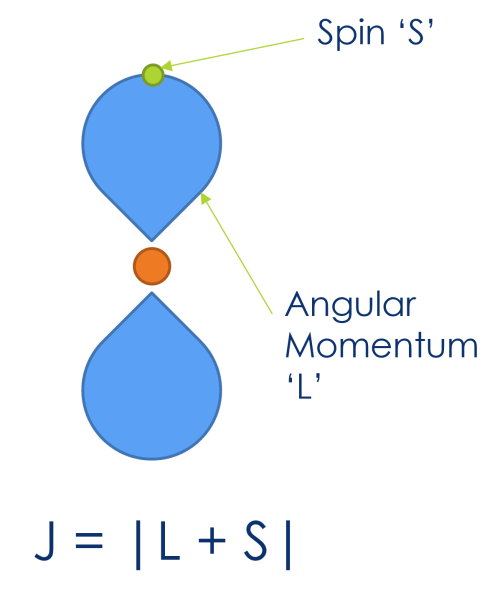
The origin of these peaks is doublets is what’s called ‘Spin-orbit coupling’
SOC describes the interaction between an unpaired electron (of spin ‘S’) and the angular momentum of it’s parent orbital (L)
These may combine to give us our total angular momentum (J) (J = | L + S |)
Electrons may therefore come from the same orbital, but have different total angular momentum (i.e. from spin up & spin down electrons)
Differing total angular momentums will result in slightly different peak energies
This is what gives us our doublet peaks

S-orbital effectively have NO orbital angular momentum (quantum number L = 0)
This is because the spherical symmetry means that the probability of finding an electron at a given position is NOT dependant on angle
More specifically, the wavefunction has no angular dependency and so the S-orbital eigenvalue for angular momentum = 0
Example – O 1s
Quantum numbers:
Principal (n) = 1
Azimuthal (l) = 0
Magnetic (m) = 0
Spin (s) = + ½ or – ½
What do you think J is?
What is J for O 1s?
J = + ½
- Using J = | L + S |
- J = | 0 + ½ | or J = | 0 – ½ |
- J = | + ½ | or | – ½ |
- J = + ½
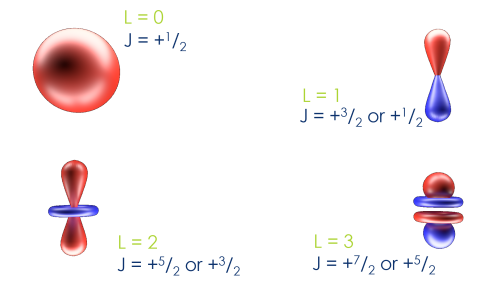
Using the same process, we can determine the total angular momentums of all of our orbitals
We use the total angular momentum to refer to the individual peaks in the following format:
Element OrbitalAngular Momentum
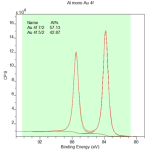
For example – Au 4f
How would we label the two peaks?
How do we label Au 4f peaks?
7/2 and 5/2
Low binding energy peak = Au 4f7/2
High binding energy peak = Au 4f5/2
2J + 1 describes the degeneracy of the states at their respective total angular momentum (sum of all m(j) states)
Individual m(j) states described as J, J-1, … , -J
m(j) = 2J + 1
J = 7/2 and 5/2
2*7/2+1 and 2*5/2+1 = 8 and 6
Area ratio = 8/6 or 4/3 (1.333r)
Measured area ratio = 57/43 (1.3336)
Therefore we have fixed ratios for each orbital type:
P-orbitals – Peak A = Peak B*2
D-orbitals – Peak A = Peak B*3/2
F-orbitals – Peak A = Peak B*4/3
These ratios are fixed – so we can use them to model spectra with overlapping doublets
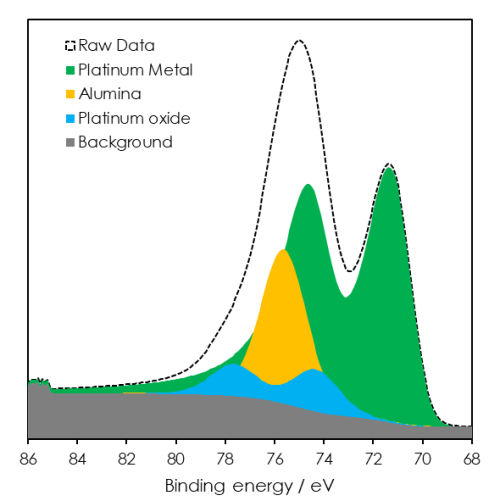
Example – Pt 4f + Al 2p overlap
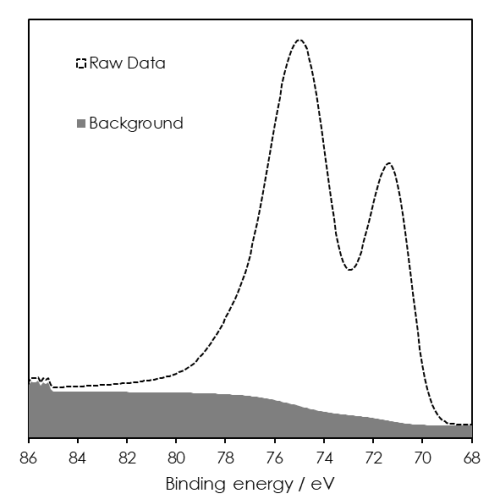
- Pt 4f5/2 peak directly overlaps with Al 2p
- Can use properties of Pt 4f7/2 to model the overlap
- Obtain additional information from peak modelling
In most cases the FWHM of doublet peaks is a constant 1:1
Very exceptions (e.g. Ti 2p), will not be touched on in this course
See our guru page on Coster-Kronig transitions for more information.
Doublet separation proportional to atomic number, principle quantum number and orbital angular momentum
When atomic mass increases, separation increases
When principle quantum number increases, separation decreases
When orbital angular momentum increases, separation decreases